Many complex networks show signs of modular structure, uncovered by community detection. Although many methods succeed in revealing various partitions, it remains difficult to detect at what scale some partition is significant. This problem shows foremost in multi-resolution methods. We here introduce an efficient method for scanning for resolutions in one such method. Additionally, we introduce the notion of “significance” of a partition, based on subgraph probabilities. Significance is independent of the exact method used, so could also be applied in other methods, and can be interpreted as the gain in encoding a graph by making use of a partition. Using significance, we can determine “good” resolution parameters, which we demonstrate on benchmark networks. Moreover, optimizing significance itself also shows excellent performance. We demonstrate our method on voting data from the European Parliament. Our analysis suggests the European Parliament has become increasingly ideologically divided and that nationality plays no role.
Subject terms:
Applied mathematics
Computer science
Statistics
At a glance
Figures
First | 1-3 of 5 | Last
View all figures
left
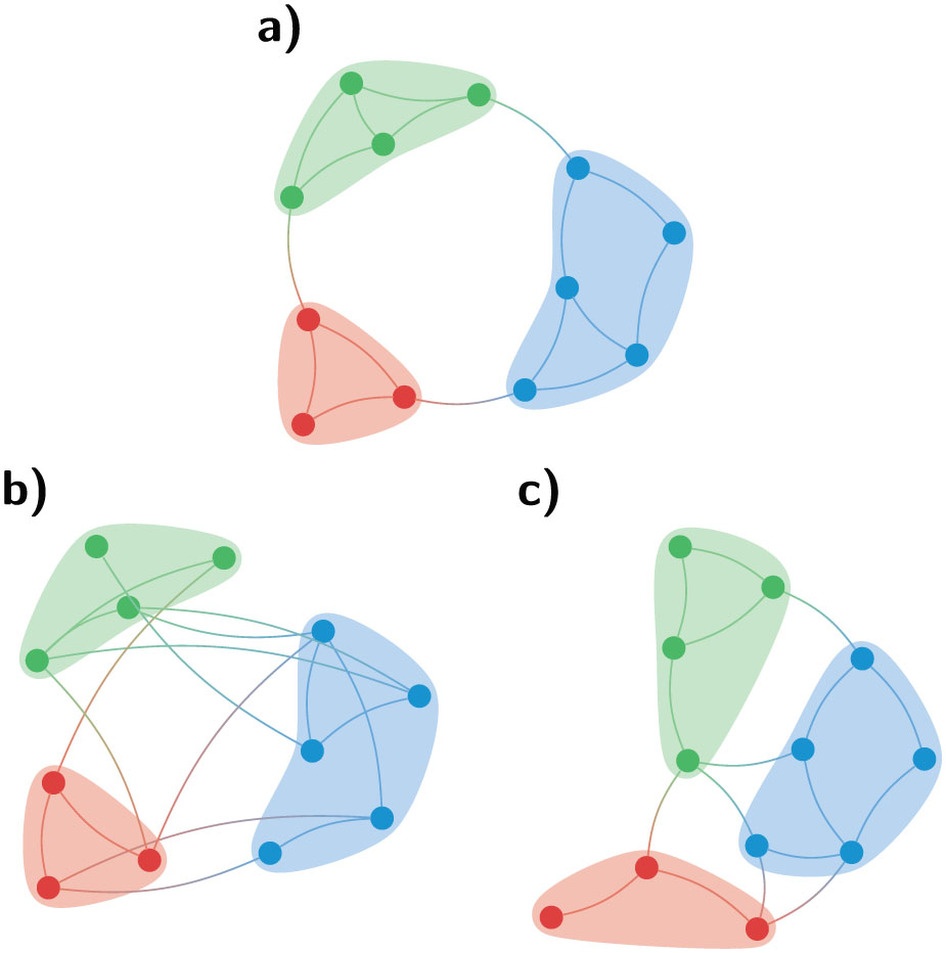
Probabilities for partitions. Figure 1
Scanning results for directed and hierarchical benchmark graphs. Figure 2
Results for ER graphs. Figure 3
Benchmark results for significance. Figure 4
Results for the European Parliament (EP). Figure 5
right
Introduction
Introduction•
Results•
Discussion•
Methods•
References•
Acknowledgements•
Author information
Networks appear naturally in many fields of science, and are often inherently complex structures. By looking at the modular structure of a network we can reduce its complexity to some extent, yielding a “bird's-eye view” of the network1, 2, 3.
Although there is no universally accepted definition of a community, there are some commonly accepted principles. We denote by G = (V,E) a graph with nodes V and edges , where the graph has n = |V| number of nodes and m = |E| number of edges, and is said to have a density of . The idea is that in general, we want to reward links within communities with some weight aij, while we want to punish missing links within communities with some weight bij. Working out this idea we arrive at
for the “cost” of a partition σ. Here Aij is the adjacency matrix, which is Aij = 1 if there is a link between i and j and zero otherwise, σi denotes the community of node i, and δ(σi, σj) = 1 if and only if σi = σj and zero otherwise. This is a slightly more simplified version of the approach by Reichardt and Bornholdt4. We will restrict ourselves here to simple, unweighed graphs.
Different weights aij and bij give rise to different methods. One can imagine for example taking the number of common neighbours as weight bij, the distance of the shortest path or some transition probability in a random walk. Many methods have been developed over the years, but the most noteworthy method is that of modularity5 which uses aij = 1 − pij, bij = pij where pij is some random null-model. It has risen to prominence because it showed encouraging results in various fields, ranging from ecology6, 7 and biology8, 9 to political science10 and sociology11.
Nonetheless modularity was found to be seriously flawed. Its biggest problem is the resolution limit12, 13, which states that modularity is unable to detect relatively small communities in large networks. We showed previously that methods that use local weights (i.e. aij and bij are independent of the graph) do not suffer from the resolution limit14, and are hence called resolution limit free. Within this framework there are relatively few methods that are resolution limit free. One such method is the Constant Potts Model14 (CPM). This model has as weights aij = 1 − γ and bij = γ where γ is a so-called resolution parameter (see next paragraph), resulting in